
Klasyfikacja modeli na podstawie ich odpowiedzi skokowych zrealizowana w środowisku MATLAB
W tym rozdziale pokazany zostanie sposób klasyfikacji obiektu na podstawie jego odpowiedzi impulsowej. Taki sposób postępowania jest najbardziej rozpowszechnionym w automatyce.
Klasyfikacja modelu polegała zrealizowaniu go w środowisku MATLAB – SIMULINK, a następnie uzyskaniu jego odpowiedzi na pobudzenie skokiem jednostkowym.
Pierwszym symulowanym obiektem był układ szeregowo połączonych członów: proporcjonalnego, inercyjnego I rzędu oraz opóźniającego.
Równanie różniczkowe takiego obiektu ma postać:
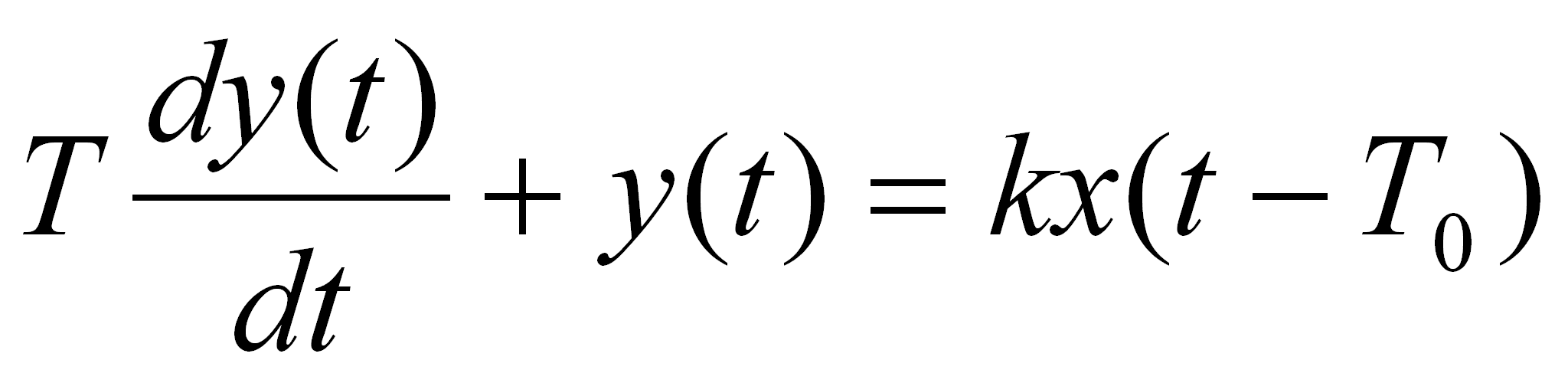 (9)
(9)
a jego transmitancja operatorowa:
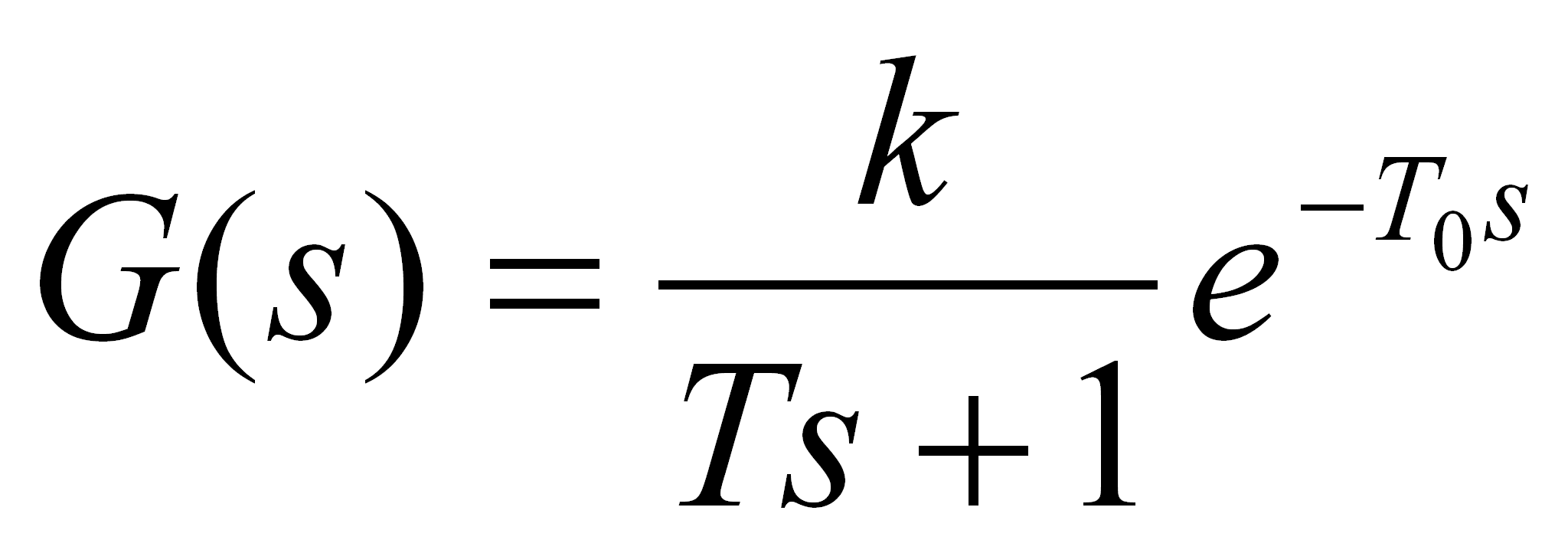 (10)
(10)
Implementacja obiektu o transmitancji operatorowej (9) w środowisku MATLAB – SIMULINK wygląda następująco:
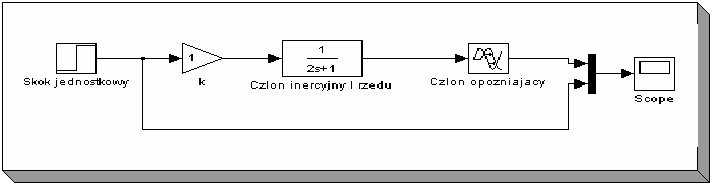
Rysunek 2.5. Realizacja obiektu o transmitancji operatorowej (9) w środowisku
MATLAB –SIMULINK
Na potrzeby symulacji przyjęto następujące wartości współczynników: k0 = 1, T = 2ms,
T0 = 0.5ms.
Pobudzenie skokiem jednostkowym oraz uzyskana odpowiedź jest przedstawiona na rysunku 2.6.
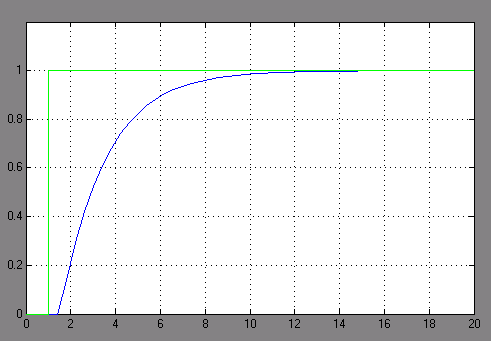
Rysunek 2.6. Pobudzenie skokiem jednostkowym oraz uzyskana odpowiedź obiektu
Z powyższego wykresu można zauważyć, że jest symulowanym układem był obiekt z wyrównaniem o parametrach
T0 = 0,5 ms i Tz = 4ms.
Drugim symulowanym obiektem był układ złożony z szeregowo połączonych członów: proporcjonalnego, oscylacyjnego i opóźniającego.
Równanie różniczkowe takiego obiektu ma postać:
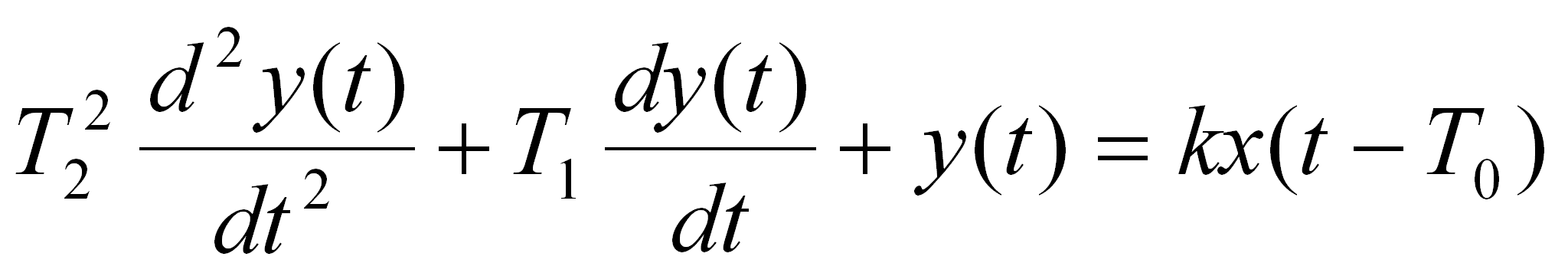 (11)
(11)
a jego transmitancja operatorowa:
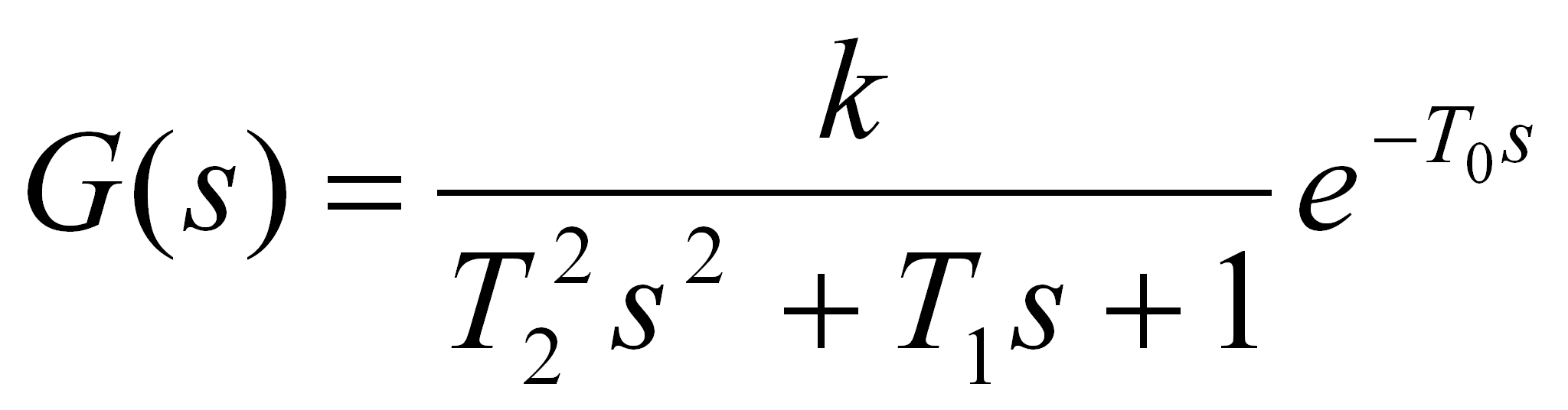 (12)
(12)
Implementacja modelu o transmitancji operatorowej (11) ma postać:
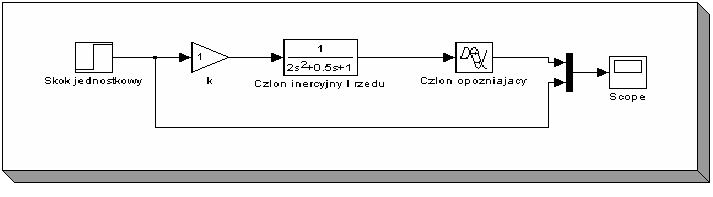
Rysunek 2.7. Realizacja obiektu o transmitancji operatorowej (11) w środowisku
MATLAB – SIMULINK
Na potrzeby symulacji przyjęto następujące wartości współczynników: k0 = 1, T22= 2ms,
T1 = 0,5 ms, T0 = 0.5ms
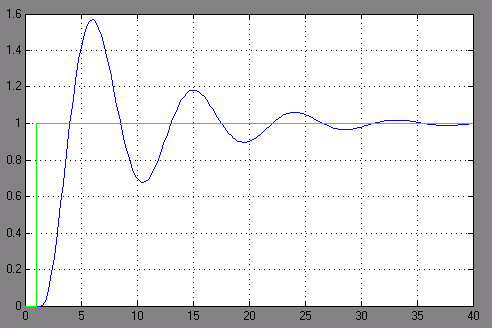
Rysunek 2.8. Pobudzenie skokiem jednostkowym oraz uzyskana odpowiedź obiektu.
Współczynniki T1 oraz T2 maja wpływ na amplitudę oraz częstotliwość oscylacji.
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.