
Część programowa modelu
Zgodnie z założeniami pracy dyplomowej określonymi w rozdziale 1, konieczne było zbudowanie modelu procesu przemysłowego, który byłby sterowny regulatorem PLC. Jako modelowany obiekt wybrano piec gazowy wyposażony w radiator do wymiany ciepła z otoczeniem.
Parametrem wejściowym modelu będzie ilość dostarczanego do niego paliwa, natomiast parametrem wyjściowym jego temperatura. Zadaniem sterownika PLC będzie ustalenie ilości dopływającego medium na poziomie zapewniającym utrzymanie stałej wartości temperatury pieca oraz przeciwdziałanie zakłóceniom mających wpływ na wartość wielkości wyjściowej .
Matematyczną reprezentacją procesu cieplnego zachodzącego wewnątrz pieca jest równanie różniczkowe I stopnia, ze współczynnikami równania zależnymi od właściwości fizycznych modelowanego pieca, które również powinny być uwzględnione podczas implementacji.
Ze względu na złożoność całego procesu przyjęto pewne uproszczenia:
Całe ciepło z pieca przekazywane jest do otoczenia, a wymiana następuje tylko na granicy radiator – powietrze,
Model jest całkowicie korpartmentowy (gradient temperatury jest jednakowy w całym obszarze modelu),
Sprawność energetyczna pieca wynosi 100%,
Temperatura otoczenia nie zmienia się w trakcie działania modelu (możliwe jest jedynie wartości temperatury otoczenia przed rozpoczęciem symulacji),
Zakłócenia sygnału wejściowego mają charakter periodyczny i są zależne od jego amplitudy.
Docelowo, do realizacji modelu posłuży środowisko LabView, natomiast w fazie wstępnej do badań i symulacji wykorzystany zostanie program MATLAB-SIMULINK.
Budowa modelu
W oparciu o opis podstawowych typów modeli procesów przemysłowych zamieszczony w podrozdziale 2.2 do implementacji programowej wybrano model obiektu z wyrównaniem opisany równaniem różniczkowym pierwszego stopnia (tabela 2.1, wiersz 2) o transmitancji operatorowej wyrażonej wzorem (4). Wybrany typ modelu używany jest w automatyce do modelowania procesów cieplnych.
Jak wspomniano w podrozdziale 3.1 wstępna realizacja modelu została przeprowadzona w środowisku MATLAB – SIMULINK.
Fizyczna reprezentacja parametrów modelu
Podczas implementacji modelu w środowiskach MATLAB – SIMULINK oraz LabView
konieczne było określenie fizycznej reprezentacji sygnału wejściowego, wyjściowego oraz parametrów fizycznych modelu.
W równaniu różniczkowym opisującym model (43) wyróżniamy następujące wielkości:
x(t) – sygnał wejściowy modelu (aktualna ilość dostarczanego paliwa [l/min.])
y(t) – sygnał wyjściowy modelu (wartość aktualnej temperatury pieca [°C])
k0 – współczynnik wzmocnienia odpowiedzialny za ilość spalanego paliwa zależny od temperatury otoczenia.
T – stała czasowa obiektu (zależna od właściwości konstrukcyjnych, wyrażona w [s]).
Sygnał wejściowy x(t) – ilość dostarczanego paliwa - obliczany jest na podstawie sygnału wyjściowego regulatora (informacji o odchyłce regulacji). W przypadku sterowania obiektem rzeczywistym za ilość dostarczanego paliwa odpowiedzialne są właściwe układy wykonawcze (pompy paliwowe o regulowanej wydajności), natomiast w przypadku symulacji procesu sterowania wielkość ta jest obliczana.
Stygnął wyjściowy y(t) - jest to rozwiązanie równania różniczkowego opisującego model przy danej wartości sygnału wejściowego (paliwa) dla aktualnej chwili czasu.
Współczynnik wzmocnienia k0 wpływa na zużycie paliwa przy procesie nagrzewania. Jego zależność od temperatury otoczenia jest proporcjonalna.
Stała czasowa obiektu T uzależniona jest od fizycznej budowy pieca, wpływa na prędkość nagrzewania się oraz studzenia. Przy obliczaniu stałej czasowej wykorzystane zostały następujące czynniki: rodzaj materiału, z którego wykonany jest radiator (różne materiały mają różne rezystancje termiczne) , masa, powierzchnia i grubość radiatora.
Zależność stałej czasowej T od powyższych współczynników przedstawia tabela 3.1.
Tabela 3.1. Zależność stałej czasowej od fizycznych współczynników modelu
| Współczynnik | Zmiana | Stała czasowa T |
| Rezystancja termiczna materiału | rośnie | rośnie |
| Masa radiatora | rośnie | rośnie |
| Powierzchnia radiatora | rośnie | maleje |
| Grubość radiatora | rośnie | rośnie |
W przypadku naszego modelu możliwy jest wybór trzech rodzajów materiału radiatora: miedzi, aluminium i żelaza.
Symulacja w programie MATLAB
Realizacja modelu w programie MATLAB – SIMULINK polegała na zbudowaniu układu będącego rozwiązaniem równania
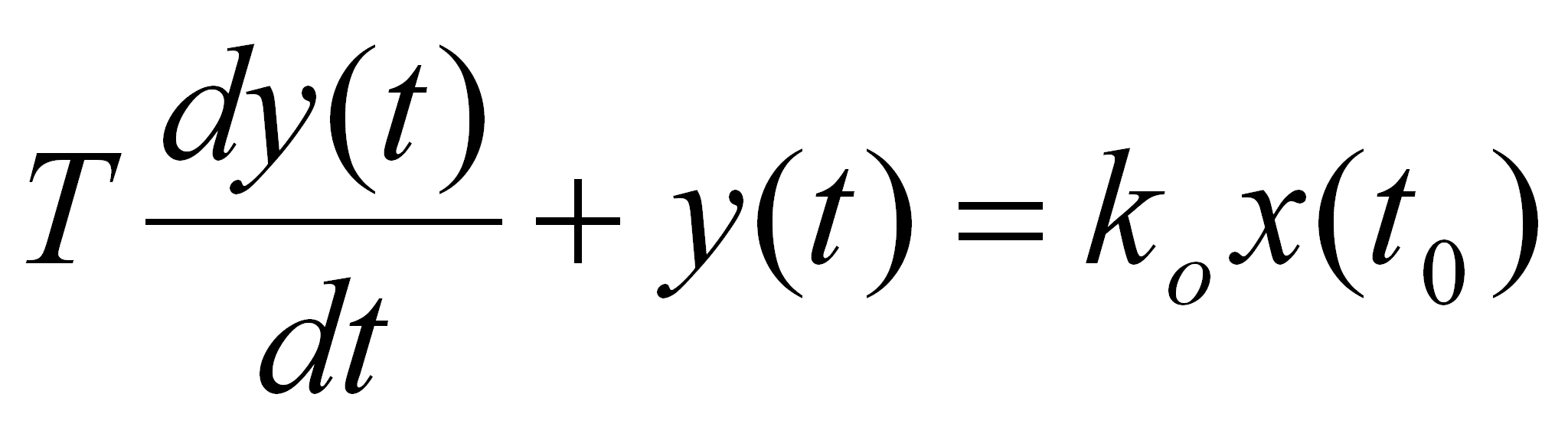 (43)
(43)
Zbudowany układ ma następujący schemat:
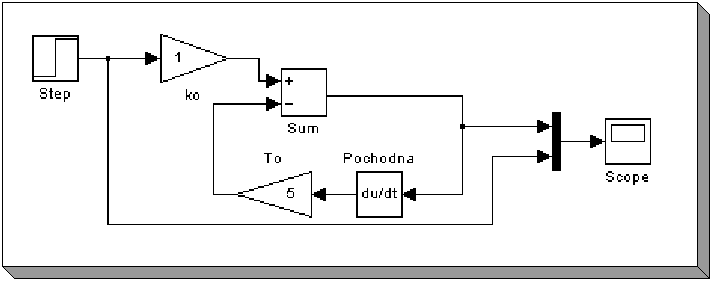
Rysunek 3.1. Układ będący rozwiązaniem równania (43).
Parametrami równania są: wzmocnienie obiektu ko (2) oraz stała czasowa obiektu To zależna od właściwości konstrukcyjnych (szczegółowy opis tej zależności znajduje się w podrozdziale 3.1.2). Na potrzeby symulacji przyjęto ko = 1, To = 5.
Zgodnie z zaleceniami dotyczącymi identyfikacji typu modelu opisanymi w rozdziale 2.3 należy pobudzić go skokiem jednostkowym, a otrzymaną odpowiedź (rysunek 3.2) porównać z zestawieniem podstawowych członów dynamicznych zawartym w tabeli 2.1.
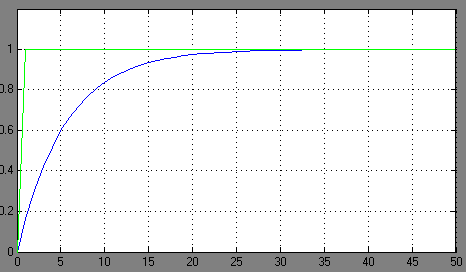
Rysunek 3.2. Pobudzenie oraz odpowiedź impulsowa modelu.
Otrzymana odpowiedź impulsowa badanego modelu odpowiada odpowiedzi członu inercyjnego pierwszego rzędu, co jest potwierdzeniem jego poprawnej implementacji.
Po modyfikacji układu w sposób przedstawiony na rysunku 3.3 możemy sporządzić tabelę pomocną do implementacji modelu w programie LabView.
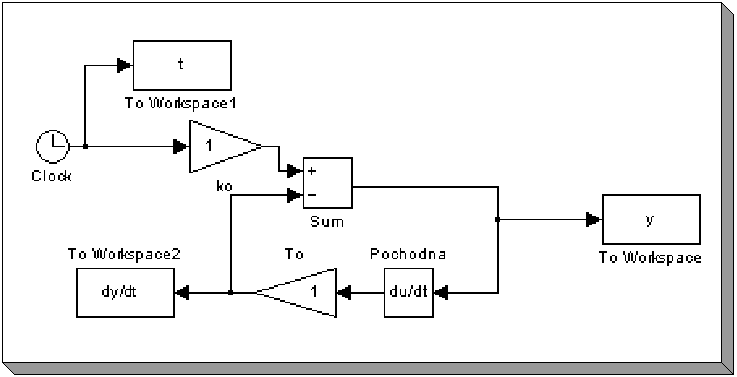
Rysunek 3.3. Zmodyfikowana struktura modelu.
Zastosowanie bloczków „To workspace” umożliwiło przesłanie wartości zmiennych do przestrzeni roboczej MATLAB’a w postaci tablicy. Pobudzeniem dla modelu jest w tym przypadku funkcja x = t, gdzie t jest aktualnym czasem symulacji.
Poniższa tabela przedstawia zestawienie zmiennych z przestrzeni roboczej.
Tabela 3.2. Zmiany wartości pobudzenia, odpowiedzi oraz pochodnej odpowiedzi w czasie.
| t = x | dy/dt | y |
| 0,0 | 0,0000 | 0,0000 |
| 0,1 | 0,0909 | 0,0091 |
| 0,2 | 0,1736 | 0,0264 |
| 0,3 | 0,2487 | 0,0513 |
| 0,4 | 0,3170 | 0,0830 |
| 0,5 | 0,3791 | 0,1209 |
| 0,6 | 0,4355 | 0,1645 |
| 0,7 | 0,4868 | 0,2132 |
| 0,8 | 0,5335 | 0,2665 |
| 0,9 | 0,5759 | 0,3241 |
| 1,0 | 0,6145 | 0,3855 |
| 1,1 | 0,6495 | 0,4505 |
| 1,2 | 0,6814 | 0,5186 |
| 1,3 | 0,7103 | 0,5897 |
| 1,4 | 0,7367 | 0,6633 |
| 1,5 | 0,7606 | 0,7394 |
| 1,6 | 0,7824 | 0,8176 |
| 1,7 | 0,8022 | 0,8978 |
| 1,8 | 0,8201 | 0,9799 |
| 1,9 | 0,8365 | 1,0635 |
Na podstawie równania (43) możemy napisać jego reprezentację w dziedzinie próbek (przy dyskretnych wartościach czasu)
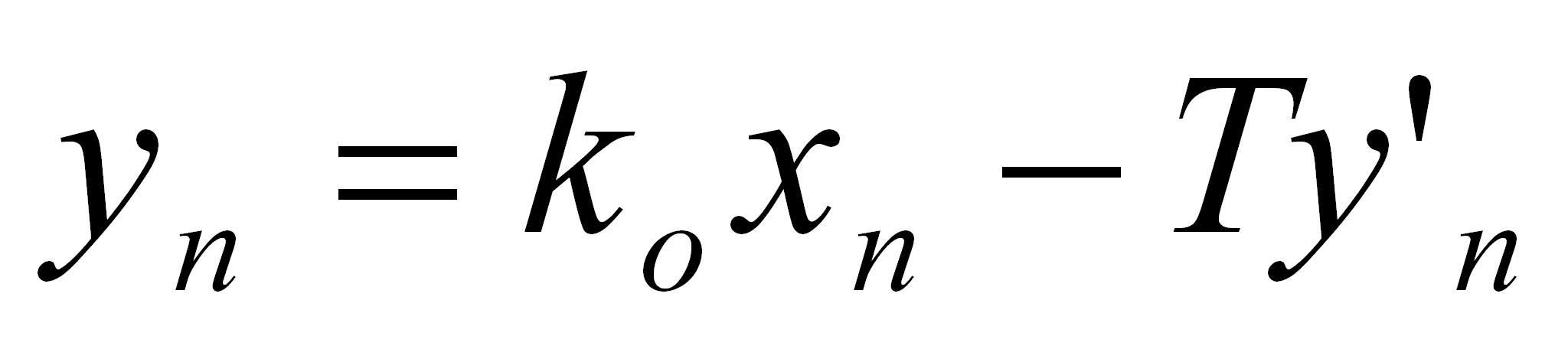 (44)
(44)
gdzie n jest numerem aktualnej próbki, natomiast
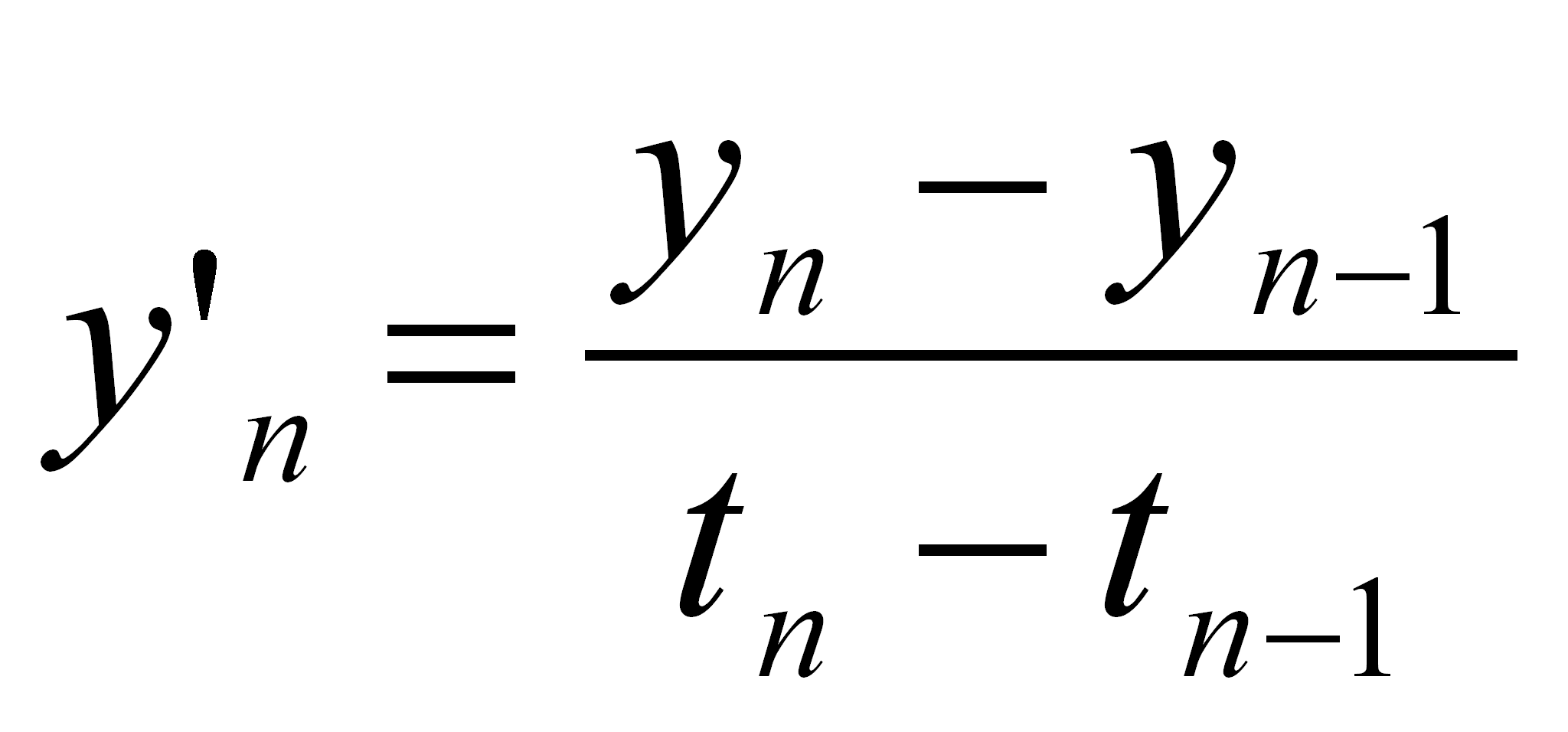 (45)
(45)
jest pochodną sygnału wyjściowego po czasie.
Podstawiając równanie (45) do (44) oraz przyjmując tn – tn-1 = Δt otrzymujemy końcową postać równania modelu
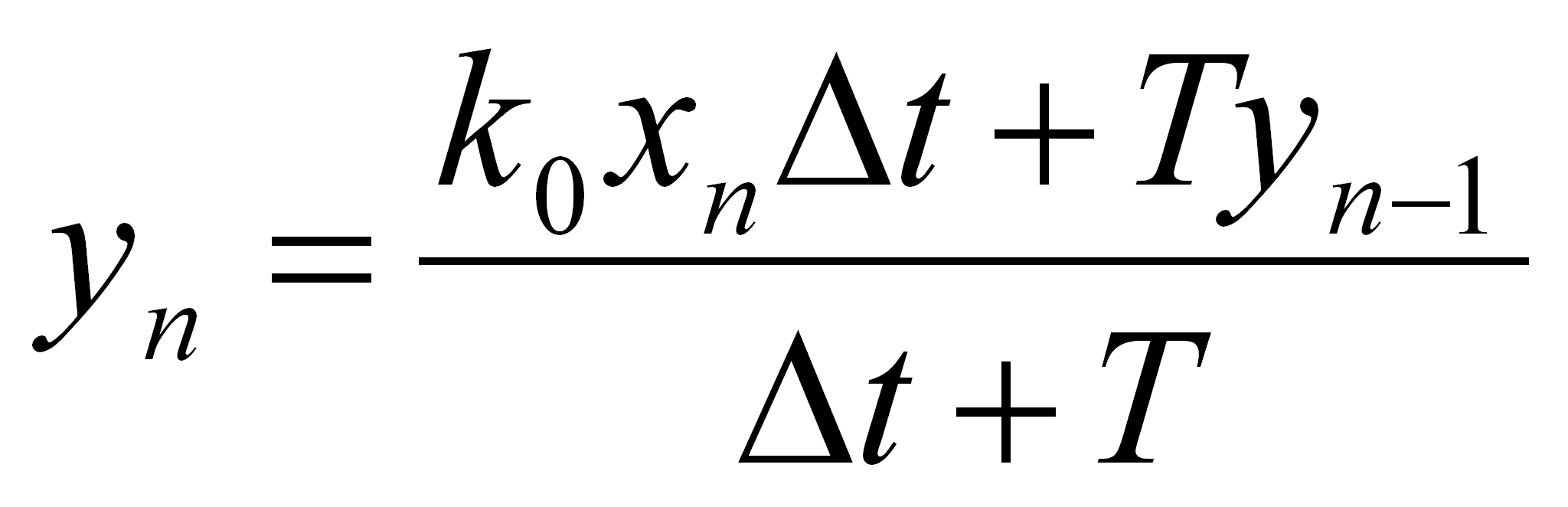 (46)
(46)
Równanie (46) zostało zaimplementowany w środowisku LabView w sposób opisany w podrozdziale 3.1.4.
Realizacja w programie LabView
Po przeprowadzeniu poprawnej symulacji w programie MATLAB – SIMULINK równanie (46) wraz z warunkami początkowymi zostało zaimplementowane w środowisku LabView.
Głównym elementem aplikacji jest formuła matematyczna zawierające równanie modelu przedstawiona na rysunku 3.4
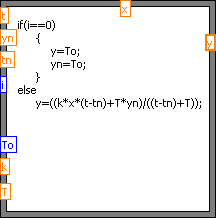
Rysunek 3.4 Formuła matematyczna zawierająca równanie modelu obiektu wraz z warunkami początkowymi.
W celu zapewnienia poprawnego działania równania należało doprowadzić do niego następujące dane wejściowe:
x – wartość wejściowa (ilość dostarczanego paliwa)
t – bieżący czas symulacji,
tn – zmienna t opóźniona o jedną próbkę,
yn – wartość sygnału wyjściowego opóźniona o jedną próbkę,
T – stała czasowa obiektu,
k – współczynnik wzmocnienia obiektu ,
To – temperatura otoczenia,
i – licznik obiegu pętli (konieczny do uwzględnienia warunków początkowych).
Sygnałem wyjściowym modelu jest aktualna wartość temperatury y.
W skład aplikacji prócz głównej formuły modelu wchodzą moduły pomocnicze takie jak:
Moduł wprowadzający sztuczne zakłócenie sygnału wejściowego. Powoduje on dodawanie do sygnału wejściowego modelu sygnału zakłócającego periodycznego o amplitudzie zależnej od amplitudy sygnału wejściowego i regulowanej częstotliwości. Fizyczną reprezentacje zakłócenia można interpretować jako zmiany kaloryczności dostarczanego paliwa.
Moduły konwertujące zakres temperatury pieca na zakres napięcia przetworników wchodzących w skład fizycznej części modelu. Użycie tych bloków było konieczne w celu konwersji wartości temperatury (-100 do +200°C) na wartość napięcia 0 – 5V i odwrotnie. Konwersja odbywała się zgodnie z poniższą zależnością:
 (47)
(47)
Gdzie y reprezentuje temperaturę, natomiast u wartość napięcia.
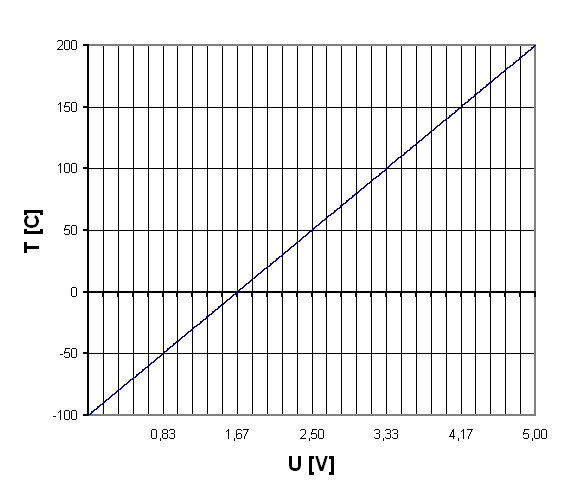
Rysunek 3.5. Charakterystyka przetwarzania temperatury na napięcie.
Moduł odpowiedzialny za obliczenie stałej czasowej obiektu, zawierający przybliżone równanie szacujące jej wartość na podstawie parametrów opisanych w podrozdziale 3.1.2
Formuła matematyczna modułu ma następującą postać:
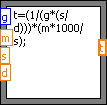
Rysunek 3.6 Formuła matematyczna obliczająca stałą czasowa obiektu.
Sygnały wejściowe formuły:
g – przewodność termiczna materiału radiatora,
m – masa radiatora ,
s- powierzchnia radiatora,
d – grubość radiatora.
Sygnałem wyjściowym modułu jest wartość stałej czasowej T.
Moduły wizualizacyjne umożliwiające prezentacje sygnałów temperatury, ilości dostarczanego paliwa i odchyłki regulacji na wykresie o stałej szerokości okna.
Za współpracę aplikacji z częścią układową modelu odpowiedzialny jest moduł komunikacyjny opisany w podrozdziale 3.2.6.
Wygląd panelu głównego aplikacji przedstawiony jest na rysunku 3.6.
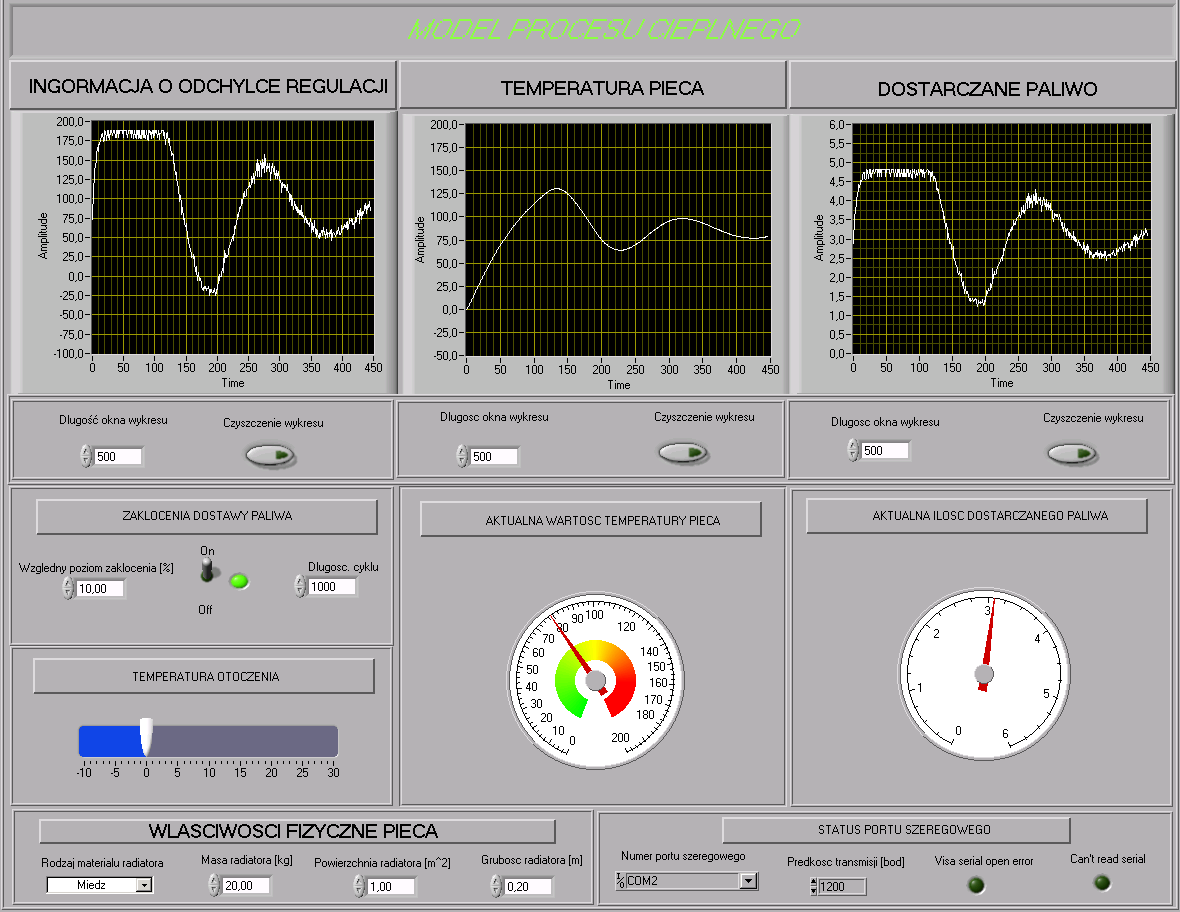
Rysunek 3.6. Panel główny aplikacji.
Panel podzielony jest na części kontrolną oraz wizualizacyjną. W skład pierwszej z nich wchodzą: wykresy przedstawiające zmiany w czasie wartości odchyłki regulacji, temperatury pieca oraz ilości dostarczanego paliwa. Długość okna wykresu wyrażona jest w sekundach i można zmieniać wpisując odpowiednią wartość w polu pod wykresem. Aktualne wartości temperatury oraz ilości dostarczanego paliwa przedstawione są również na wskaźnikach analogowych.
Sekcja „Zakłócenia dostawy paliwa” zawiera pola umożliwiające wprowadzenie wartości amplitudy oraz długości cyklu sygnału zakłócającego oraz przełącznik aktywujący zakłócenie.
Poniżej znajduje się suwak umożliwiający ustawienie temperatury otoczenia pieca. Wartość tą należy ustawić przed uruchomieniem aplikacji.
W lewym dolnym rogu znajdują się pola edycyjne umożliwiające wprowadzenie parametrów fizycznych pieca opisanych w podrozdziale 3.1.2. Wartości te również należy ustawić przed uruchomieniem aplikacji.
Sekcja „Status” portu szeregowego” umożliwia wybór portu na którym pracuje część sprzętowa modelu wraz z jego prędkością transmisji (zgodnie z opisem zawartym w podrozdziale 3.2.3 prędkość jest ustalona na 1200 bod) oraz dwie kontrolki sygnalizacyjne status urządzenia.
Wymagania sprzętowe modelu
Zaimplementowany przez nas w środowisku LabView model jest równaniem różniczkowym, posiadającym wejście sygnału przetwarzanego oraz wyjście jego odpowiedzi na ten sygnał. Sterowanie modelem będzie się odbywało poprzez regulator PID operującym na sygnale elektrycznym, którego wartość wyjściowa również będzie w postaci sygnałowej.
W celu umożliwienia komunikacji pomiędzy tymi obiektami należy zastosować układy przetwornikowe:
Przetwornik analogowo cyfrowy na wejściu modelu,
Przetwornik cyfrowo – analogowy na wyjściu modelu.
Realizacja części sprzętowej modelu została opisana w punkcie 3.2
komentarze
Copyright © 2008-2010 EPrace oraz autorzy prac.